ara resolver los dos problemas que el procedimiento usual de medición de la pobreza de ingresos desatiende: la variación de necesidades con la edad y el sexo; y las economías de escala en el consumo doméstico (véase entrega del 22/4/11), Alejandro Marín partió de la Canasta Normativa de Satisfactores Esenciales (CNSE) de Coplamar con el propósito inmediato de corregir uno de sus defectos: haberse limitado a un único cálculo: el del costo de una canasta para el hogar promedio nacional. Marín calculó el costo de la CNSE para tamaños de hogar con rango de uno a 10 personas y para casi todas las combinaciones posibles de estructura de sexo y edad para cada tamaño de hogar (un total de 142 combinaciones). Pero no llegó a una fórmula sintética, aunque estimó las elasticidades de los costos normativos del tamaño de hogar (qué tanto aumenta el costo de la CNSE a medida que aumenta el tamaño del hogar) y encontró que ésta era invariablemente menor que la unidad, indicando la presencia de economías de escala (EE). En Boltvinik y Marín (La canasta normativa de satisfactores esenciales de la Coplamar. Génesis y desarrollos recientes, Comercio Exterior, vol. 53, N° 5, mayo de 2003, pp. 473-484) tampoco llegamos a una fórmula sintética. En un trabajo realizado en 20071 llegué a una fórmula sintética que toma en cuenta economías de escala (EE) y equivalencias entre diferentes grupos de personas.

El proceso lógico que permite llegar a lo que se podría denominar el procedimiento Marín-Boltvinik es el siguiente. La línea de pobreza (LP) de un hogar determinado es igual a la suma del costo de dos tipos de bienes y servicios (para abreviar, bienes): bienes familiares (BF) y bienes individuales (BI). Es característica de los BF que su uso por una persona no excluye a otras de usarlo (simultánea o secuencialmente), mientras que los BI se caracterizan porque su uso excluye a otras personas: nadie puede usar la ropa que yo estoy usando (cada uno necesita usar alguna ropa casi todo el día). Los BF son de dos tipos: bienes familiares fijos (BFF), los que no necesitan incrementarse cuando crece el tamaño de la familia (dentro de ciertos rangos), y bienes familiares variables (BFV), los cuales sí se incrementan, pero generalmente menos que proporcionalmente, con el tamaño del hogar. Por tanto el costo de la CNSE o línea de pobreza (LP) es la suma del costo de los BI y de las dos categorías de bienes familiares: LP= BI+ BFF+ BFV. Las economías de escala derivan de ambos tipos de bienes familiares. Adoptando los grupos de individuos usados en la definición de la CNSE, Marín calculó el costo de los BI para seis grupos de individuos: adultos masculinos, adultos femeninos, niños, niñas, bebés masculinos, bebés femeninos. Los bebés son definidos como los menores de tres años de edad; los niños de tres a 14 años de edad, y los adultos de 15 años y más. Los costos de los BI de cada grupo se suelen re-expresar como la proporción que representan del costo de los BI de un varón adulto y se conocen como unidades varón adulto equivalente (VAE). Las equivalencias en VAE de cada grupo de personas es la siguiente: hombre adulto: 1.00; mujer adulta, 0.81; niño 0.58; niña, 0.54; y bebé de cualquier sexo, 0.43, con lo cual se expresa que, por ejemplo, el costo individual de un niño varón es 58 por ciento de un hombre adulto. Por tanto, el costo de los BI del hogar puede expresarse como el producto del costo de un VAE (llamémosle c a dicho costo) por el número de VAE en el hogar: BI = cVAE.

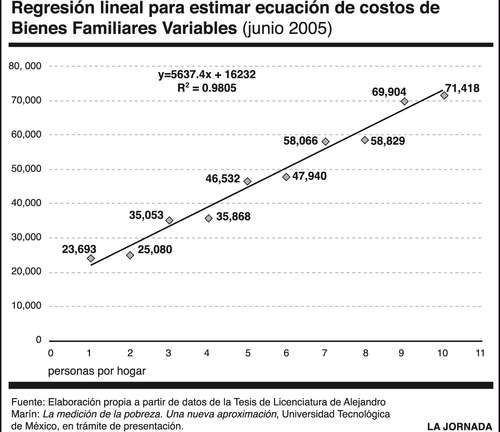
Marín identificó y calculó el costo de los BFF (llamémosle d). Es decir, hasta aquí tenemos que LP = d+ cVAE+ BFV. En cuanto a los BFV, Marín calculó su costo para los tamaños de hogares de 1 a 10 integrantes, información a partir de la cual, aplicando una regresión lineal (que resultó la que mejor ajustó), estimé la ecuación de costos de los BFV, tal como se representa en la gráfica. Dicha ecuación, sustituyendo los valores específicos para 2005 de la gráfica por letras, y expresando el número de personas por P, puede expresarse como BFV= e + bP. De esta manera, nuestra nueva ecuación del costo de la CNSE o LP para cada hogar será: LP = d + e + bP + cVAE. La cual, al definir a = d + e, queda convertida en la ecuación final: LP = a + bP + cVAE.

Esta ecuación expresa que hay un costo fijo en el consumo del hogar (a, formado por el costo de los BFF, d y el término fijo, ordenada al origen, de la ecuación de los BFV, e), un costo (b) por cada persona del hogar, y un costo (c) por cada varón adulto equivalente del mismo. Las constantes a, b y c son iguales para todos los hogares, pero P, número de personas y VAE, número de varones adultos equivalentes, al variar entre hogares, con lo cual llegaríamos a las 142 combinaciones que calculó Marín. La fórmula permite convertir el cálculo en un cálculo para cada hogar. A diferencia de la mayor parte de las soluciones que se han planteado en la materia (algunas de las cuales se discuten en el artículo Boltvinik-Marín citado), la aquí descrita es una solución normativa, que se deriva de la CNSE de Coplamar.

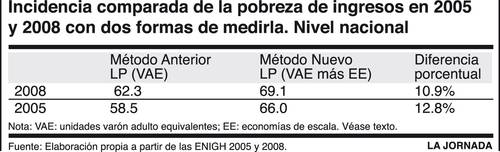
La presencia en la fórmula de dos variables independientes (P y VAE) refleja un hecho muy importante a veces olvidado. En ciertas necesidades (aquellas satisfechas con BFV) los individuos cuentan igual, porque sus necesidades son equivalentes cuantitativamente. Pero en otras necesidades (las satisfechas con BI) cuentan de manera diferente, porque sus necesidades difieren cualitativa y/o cuantitativamente. En el Cuadro se ejemplifica el impacto que la adopción del nuevo procedimiento tiene en la medición de la pobreza con datos de 2008 y 2005 a nivel nacional. El efecto parece más amplio de lo que seguramente es atribuible al cambio de procedimiento en sí mismo, porque Marín también introdujo algunos cambios en la definición de la CNSE que tienden a elevar su costo pero que son sin duda correctos. El nuevo procedimiento impedirá la ilusión de que la pobreza disminuye como resultado de la disminución del tamaño de los hogares, como se argumentó en la entrega anterior.

¹ Julio Boltvinik, Una propuesta metodológica para México de acuerdo con los requerimientos definidos en la Ley para el Desarrollo Social (indebidamente cambiado el título a Principios de medición multidimensional de la pobreza) en Julio Boltvinik, et al., Medición multidimensional de la pobreza en México, Coneval-El Colegio de México, pp. 43-279.

http://www.julioboltvinik.org • jbolt@colmex.mx