l indicador usual de ingresos (para la medición de la pobreza) es el ingreso per cápita del hogar (así lo establece también la Ley General de Desarrollo Social), que se compara con una línea de pobreza (LP) expresada también en términos per cápita. Pero el ingreso per cápita es un indicador muy defectuoso que niega la existencia (o importancia) de dos hechos: 1) Las necesidades cambian con la edad y otras características de las personas. Por ejemplo, los requerimientos alimentarios cambian mucho de acuerdo con la edad, sexo, tipo de actividad, etcétera. 2) En el consumo del hogar hay economías de escala (el consumo crece al crecer el hogar pero menos que proporcionalmente) en algunas dimensiones como espacio de la vivienda, equipamiento y mobiliario, consumo de electricidad y de combustible. Estos hechos implican que el uso del ingreso per cápita es un error mayor, pues distorsiona la identificación de los hogares pobres: subestima la pobreza de los hogares de pocos integrantes y sobrestima la de hogares grandes, sobre todo si tienen muchos menores.

Los dos problemas se han tratado de resolver construyendo reglas o ecuaciones que expresan la LP de un hogar como una función (no proporcional) de su tamaño y que toma en cuenta las diferentes necesidades por edad y a veces por sexo también. En general se conocen como equivalencias o unidades equivalentes. Una de estas ecuaciones es la usada por la Organización para la Cooperación y el Desarrollo Económico (OCDE). Con ésta, la LP de un hogar cualquiera, dada la LP de un adulto que vive solo, denotada como LP1,0 (los superíndices expresan, antes de la coma, el número de adultos adicionales y el de niños después de ella) es calculada con la fórmula siguiente: LPA,N = LP1,0 [1+ 0.7A + 0.5N], donde A es el número de adultos adicionales al primero y N el de niños. Por lo tanto, la LP de un hogar de 6 personas con 3 adultos y 3 niños será LP3,3 = LP1,0 [1+ 0.7(2) + 0.5(3)] = 3.9 LP1,0, lo cual está muy lejos de 6LP1,0 que resultaría de calcularla con el enfoque per cápita.

Este último enfoque subestima la incidencia (e intensidad) de la pobreza de los hogares pequeños y/o sobrestima la de los hogares grandes, y a través del tiempo sobrestimará el descenso (subestimará el aumento) de la pobreza si el tamaño del hogar está disminuyendo, como ocurre en México. En efecto, el tamaño promedio de los hogares era 4.93 en 1989 y de 3.95 en 2006 de acuerdo a las ENIGH (Encuestas nacionales de Ingresos y gastos de los Hogares). La composición por edades del hogar también ha cambiado rápidamente. En 1989 el hogar promedio tenía 1.51 niños (menores de 12 años de edad) y esta cifra decreció a 0.96 en 2006, de 30.6 por ciento a 24.3 por ciento del total de miembros del hogar, mientras los adultos decrecieron relativamente menos, de 3.42 a 2.99 (aumentando su peso relativo en la población de 69.4 por ciento a 75.7 por ciento). Aplicando la fórmula de la OCDE al hogar promedio en ambos años, obtenemos los siguientes resultados: 4.15LP1,0 en 1989 y 3.58LP1,0 en 2006 lo cual significa un decrecimiento en la LP del hogar promedio de 13.9 por ciento, mientras que usando los cálculos per cápita el cambio será de 4.93LP1,0 a 3.95 LP1,0, decrecimiento de 19.9 por ciento, el cual sobrestima el ‘verdadero’ decrecimiento en el costo de vida por hogar promedio en 6 puntos porcentuales (43.2 por ciento del decrecimiento real).

Agravando esta causa de sobrestimación del decrecimiento en la LP del hogar promedio (y por tanto de sobrestimación en el descenso de la pobreza cuando ésta está bajando), está el hecho de que para obtener una línea de pobreza alimentaria per cápita, que es parte de la línea de pobreza total, es una práctica común (de la Cepal y de Inegi-Cepal, de donde tomó la canasta normativa alimentaria el Comité Técnico de la Pobreza y la siguió usando el Coneval) calcularla para el hogar promedio de un año determinado, cálculo que depende de la estructura de edades y sexos de la población (la pirámide poblacional). Pero esta pirámide cambió mucho en los 17 años de 1989 a 2006: la proporción de niños en el hogar promedio cayó de 30.6 por ciento a 24.3 por ciento y la de adultos subió de 69.4 por ciento a 75.7 por ciento. Los niños varones menores de 12 años de edad tienen, como promedio simple, un requerimiento de energía de 1,660 kcal por día, mientras que los requerimientos promedio de los adultos es de 2,478 kcal por día. Cuando estos ponderadores son aplicados a los requerimientos calóricos del hogar promedio hay un incremento modesto pero significativo en los requerimientos calóricos promedio en 2006 con respecto a 1989, de 2.6 por ciento. Cuando ambas omisiones (la del modificado requerimiento calórico y la de no tomar en cuenta las economías de escala en el hogar) son corregidas, la LP alimentaria correcta del hogar promedio en 2006 resultaría ser es 8.6 por ciento más alta que lo calculado por el Comité Técnico y Coneval.

Con las LP per cápita, dos hogares con el mismo número de miembros tendrán la misma LP por hogar, al margen de su composición por sexo y edad, lo que es altamente distorsionante. Tomemos dos hogares con seis miembros cada uno, uno con 4 adultos y 2 niños, y el otro con 4 niños y 2 adultos. Si su ingreso corriente total es el mismo, serán considerados como si estuvieran en una situación idéntica usando las LP per cápita. Pero usando las líneas de pobreza que reflejen sus requerimientos nutricionales proporcionales, que son 2,177 kcal por persona en el primero y 1,877 kcal por persona en el segundo, una diferencia de 16 por ciento, resulta obvio que con el mismo ingreso del hogar el primer hogar estaría mucho peor.

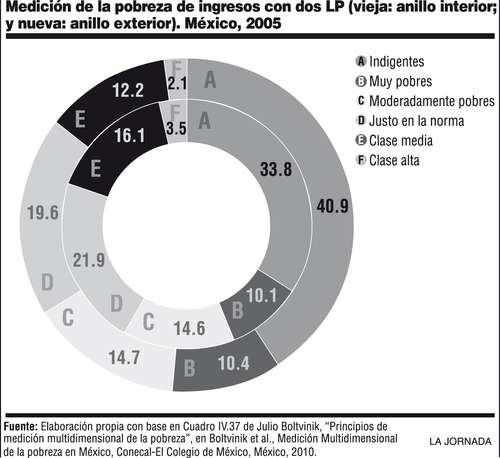
Una opción para resolver estos problemas (aparte de revisar la canasta alimentaria) sería aplicar una solución institucional como la de la OCDE. Pero ésta es una solución sub-óptima porque no distingue explícitamente entre bienes individuales y familiares (en éstos últimos es donde se presentan las economías de escala) y es totalmente empirista, tanto en la definición de la LP como en la fórmula de equivalencias utilizada (antes referida). Una opción más consistente con el enfoque normativo adoptado en el MMIP consiste en aplicar los resultados de la tesis de licenciatura de Alejandro Marín, cuyos puntos principales fueron sintetizados en un artículo que escribimos juntos¹. En próxima entrega explicaré tal solución y sus implicaciones empíricas. Adelanto resultados para 2005 en la Gráfica (donde llamo nueva LP a la que incorpora economías de escala y diferencias de necesidades por edad y sexo).

1 Julio Boltvinik y Alejandro Marín, La canasta normativa de satisfactores esenciales de Coplamar. Génesis y desarrollos recientes, Comercio Exterior, vol. 53 , N° 5, mayo de 2003, pp.473-484.

http://julioboltvinik.org • jbolt@colmex.mx